Conical helix
Object type: Space curve
Definition
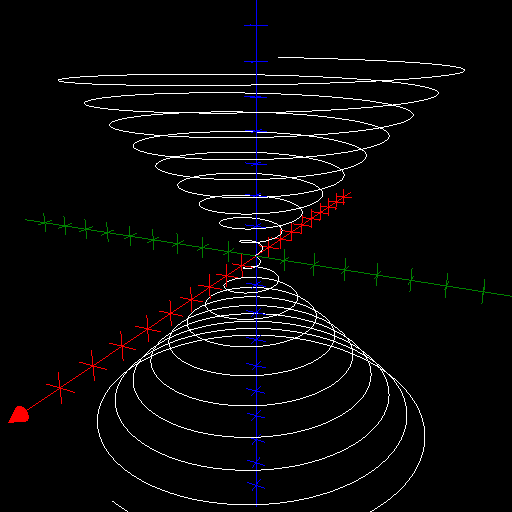
In $\mathbb{R}^3$, an elliptic conical helix is an image $\mathbf{r} (\mathbb{R})$ where $$\mathbf{r}(t) = \underline{\mathbf{e}}\begin{pmatrix}a t \cos{t} \\b t \sin{t}\\ct\end{pmatrix}, \quad\quad\forall t\in\mathbb{R},$$ for some constants $a, b, c > 0$. If $a = b =: r$, we have a circular conical helix of radius $r$. Notice that the elliptic (circular) conical helix is a subset of the elliptic (circular) cone $$\left(\frac{x}{a}\right)^2 + \left(\frac{y}{b} \right)^2 = \left(\frac{z}{c}\right)^2$$ which explains the name of the curve. Below a circular conical helix with $r = c = 1/10$ is shown.
Arc Length
The arc length from the origin to parameter value $t > 0$ is $$L(t) = \int_0^t {\sqrt{ \left(a\cos\tau-a\tau\sin\tau\right)^2+\left(b\sin\tau+b\tau\cos\tau\right)^2+c^2}d\tau}. $$ In the special case of a circular conical helix, the arc length is $$L(t) = \int_0^t { \sqrt{r^2+c^2+r^2\tau^2} d\tau} = \frac{xt}{2}\sqrt{1+\frac{r^2t^2}{x^2}} + \frac{x^2}{2r} \text{arcsinh}\frac{rt}{x}$$ where $x := \sqrt{r^2 + c^2}$.
Trivia
It is tempting to create a colourful and fuzzy conical helix.