Helicoid
Object type: Surface
Definition
The helicoid is the image $\mathbf{r}(\mathbb{R}^2)$ where $$\mathbf{r}(u,v) = \underline{\mathbf{e}}\begin{pmatrix}u\cos v\\u\sin v\\v\end{pmatrix}.$$ Below, the image $\mathbf{r}(\left[-\pi,\pi\right]\times \mathbb{R})$ is shown.
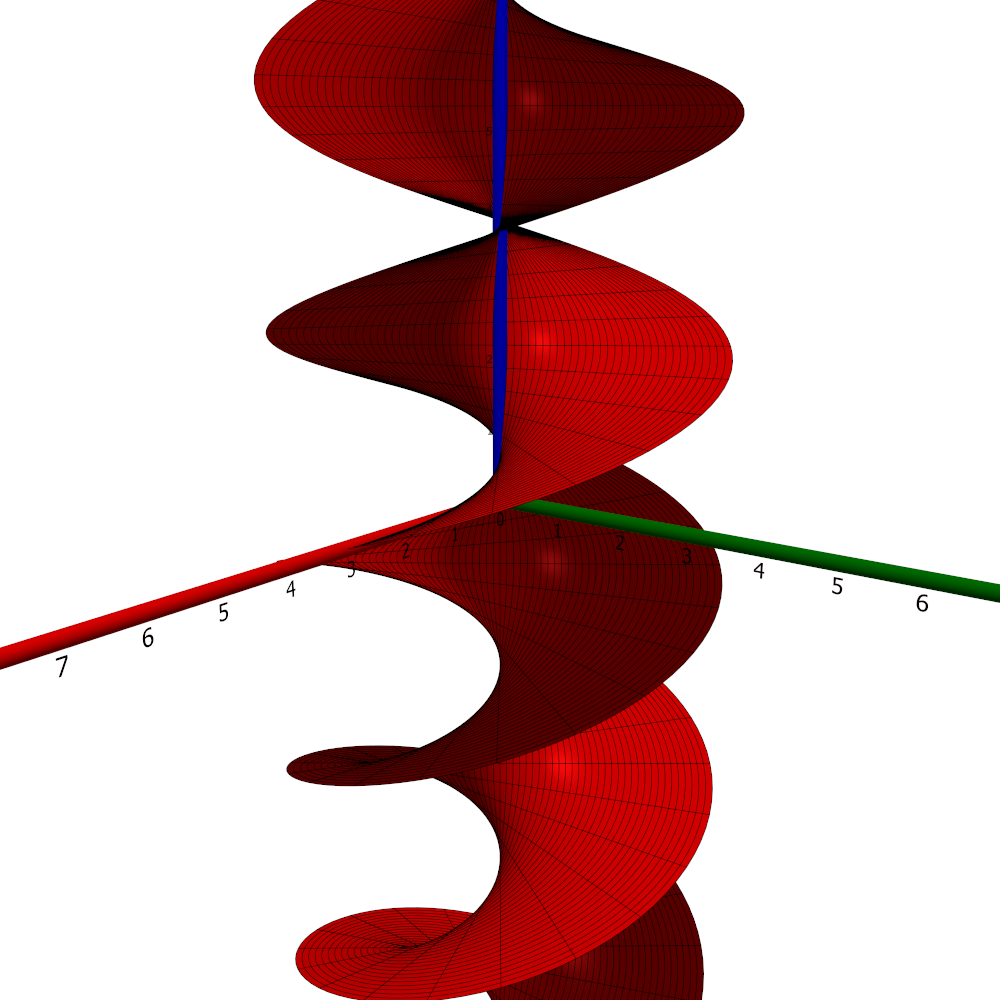
Properties
The following properties are with respect to the parameterisation given above.
Parameter-curve tangent vectors
The parameter-curve tangent vectors are $$\mathbf{r}_u(u,v) = \underline{\mathbf{e}} \begin{pmatrix}\cos v\\\sin v\\0\end{pmatrix}, \quad\quad \mathbf{r}_v(u,v) = \underline{\mathbf {e}}\begin{pmatrix}-u\sin v\\u\cos v\\1\end{pmatrix}.$$
Standard unit normal
The standard unit normal vector field is $$\mathbf{\hat{N}}(u,v) = \frac{1}{\sqrt{1+u^2}} \underline{\mathbf{e}}\begin{pmatrix}\sin v\\-\cos v\\u\end{pmatrix}.$$
Area element
The area element is $$dA = \sqrt{1+u^2}~dudv.$$
First fundamental form
The first fundamental form of the helicoid is $$\mathcal{F}(u,v) = \begin{pmatrix}1&&0\\0&&1 + u^2\end{pmatrix}.$$
Second fundamental form
The second fundamental form is $$\mathcal{M}(u,v) = \frac{-1}{\sqrt{1+u^2}}\begin{pmatrix} 0&&1\\1&&0\end{pmatrix}.$$
Christoffel symbols
The Christoffel symbols are $$\Gamma^1_{\alpha\beta}(u,v) = \begin{pmatrix}0&&0\\0&&-u\end {pmatrix}, \quad\quad \Gamma^2_{\alpha\beta}(u,v) = \frac{u}{1+u^2}\begin{pmatrix}0&&1\\1&&0 \end{pmatrix}.$$
Curvatures
The principal curvatures are $$\kappa_1 = \frac{1}{1+u^2}, \quad\quad \kappa_2 = \frac{-1}{1+u^2}$$ with the corresponding principal directions $(1,0)$ and $(0,1)$. Therefore, the Gaussian and mean curvatures are $$K = \frac{-1}{\left( 1+u^2\right)^2}, \quad\quad H = 0.$$ Thus, the helicoid is a minimal surface (that is, a surface of zero mean curvature).
Examples
Consider a (thread-like) bar of length $L > 0$ attached at its centre to a motor and used as a propeller on a vehicle. The vehicle is moving with unit speed along the $z$ axis and the propeller is perpendicular to this axis, with its centre at the origin at the origin of time. If the propeller is rotating in the positive sense (with respect to the velocity of the vehicle) with unit angular frequency, then the surface in space traced out by the propeller from the origin of time to time $t_0$ is $\mathbf{r}(\left[-L,L\right]\times\left [0,t_0\right])$.
Generalisations
The image of $$(u,v) \mapsto \underline{\mathbf{e}}\begin{pmatrix}au\cos v\\bu\sin v\\v\end{pmatrix}$$ is naturally called an elliptic helicoid. If $a = b$ this reduces to the standard helicoid (scaled the same amount in the $x$ and $y$ directions).
