Hyperbola
Object type: Plane curve
Definition
In $\mathbb{R}^2$, a hyperbola $H$ is a set of points satisfying the equation $$\left(\frac{x}{a}\right)^2 - \left(\frac{y}{b}\right)^2 = 1$$ for some $a, b > 0$. In the figure below, $a = b = 1$.
Notice that the hyperbola is an unbounded set, consisting of two disconnected parts, which we denote $H_+$ and $H_-$, where $$H_+ = \left\{ (x,y) \in H : x > 0\right\}$$ and $$H_- = \left\{(x,y) \in H : x < 0\right\}.$$
Parameterisations
The hyperbola may be parameterised by the hyperbolic functions. Indeed, $H_+ = \mathbf{r}(\mathbb{R})$ where $$\mathbf{r}(t) = \underline{\mathbf{e}}\begin {pmatrix}a \cosh{t} \\ b \sinh{t}\end{pmatrix}, \quad\quad \forall t \in \mathbb {R}.$$ It is obvious that every $\mathbf{r}(t)$ satisfies the defining equation for the hyperbola due to the hyperbolic identity $\cosh^2 {t} - \sinh^2 {t} = 1$. $H_-$ is parameterised by changing sign on the $x$ coordinate.
Properties
From the defining equation, it is evident that the lines $x/a = \pm y/b$ are asymptotic to the hyperbola.
Curvature
The curvature function for the hyperbolic branch $H_+$ using its standard hyperbolic parameterisation is $$\kappa(t) = \frac{ab}{\left(a^2 \sinh^2 {t} + b^2 \cosh^2 {t}\right)^{3/2}}.$$ In particular, if $a = b = 1$ we have $$\kappa(t) = \frac{1}{\left(\cosh{\left(2t\right)}\right)^{3/2}} = \text{sech}^{3/2}(2t). $$
Examples
A distant comet making a fly-by around a star will trace out a hyperbola. Notice the physical significance of the asymptotic behaviour of the curve: when the comet is far from the star, it will not experience any forces, and so it will travel with constant velocity in a straight line.
In Rutherford scattering, alpha particles are sent towards a positive gold nucleus. The trajectories of the alpha particles will also be hyperbolas. In fact, hyperbolas are typical for unbounded trajectories goverened by an inverse-square law.
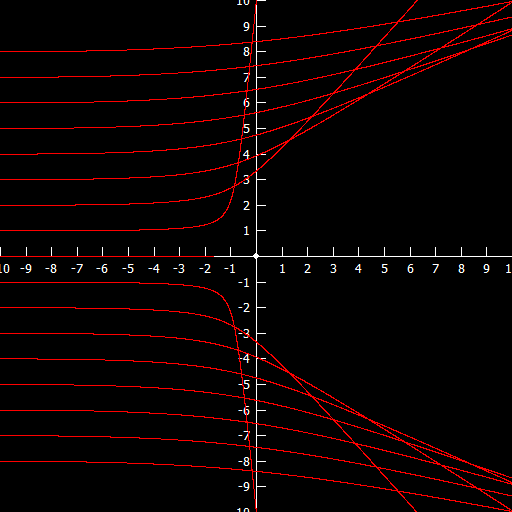
The inverse proportionality
A curve $$y = \frac{c}{x},$$ where $c\ne 0$, is a hyperbola. Specifically, it is a hyperbola, as defined above, with $a = b$ but rotated 45° about the origin. The most intuitive way to see this is to introduce a new basis $\f$ in $\R^2$ by $$\f = \frac{1}{\sqrt{2}}\basis\begin{pmatrix} 1&&1\\-1&&1\end{pmatrix}.$$ Then, if the new coordinates are $X,Y$, we have $$\basis\begin{pmatrix} x\\y\end{pmatrix}=\f\begin{pmatrix}X\\Y\end{pmatrix}\Leftrightarrow\begin{pmatrix}x\\y\end{pmatrix} =\frac{1}{\sqrt{2}}\begin{pmatrix}1&&1\\-1&&1\end{pmatrix}\begin{pmatrix}X\\Y\end{pmatrix}.$$ Hence, $$\left(\frac{x}{a}\right)^2 - \left(\frac{y}{a}\right)^2 = 1 \Leftrightarrow \frac{2}{a^2}XY=1,$$ that is, $Y = c/X$ with $c=a^2/2$.
Below, the graph $y = 1/2x$ is shown.
Below, the hyperbola $x^2 - y^2 = 1$ is shown together with the new basis vectors $\mathbf{f}_1$ and $\mathbf{f}_2$.
