Parabolic cylinder
Object type: Surface
Definition
In $\mathbb{R}^3$, a parabolic cylinder is a set of points $(x,y,z)$ satisfying the equation $$y = a x^2$$ for some $a \ne 0$. Below, a part of a parabolic cylinder with $a = 1/8$ is shown.
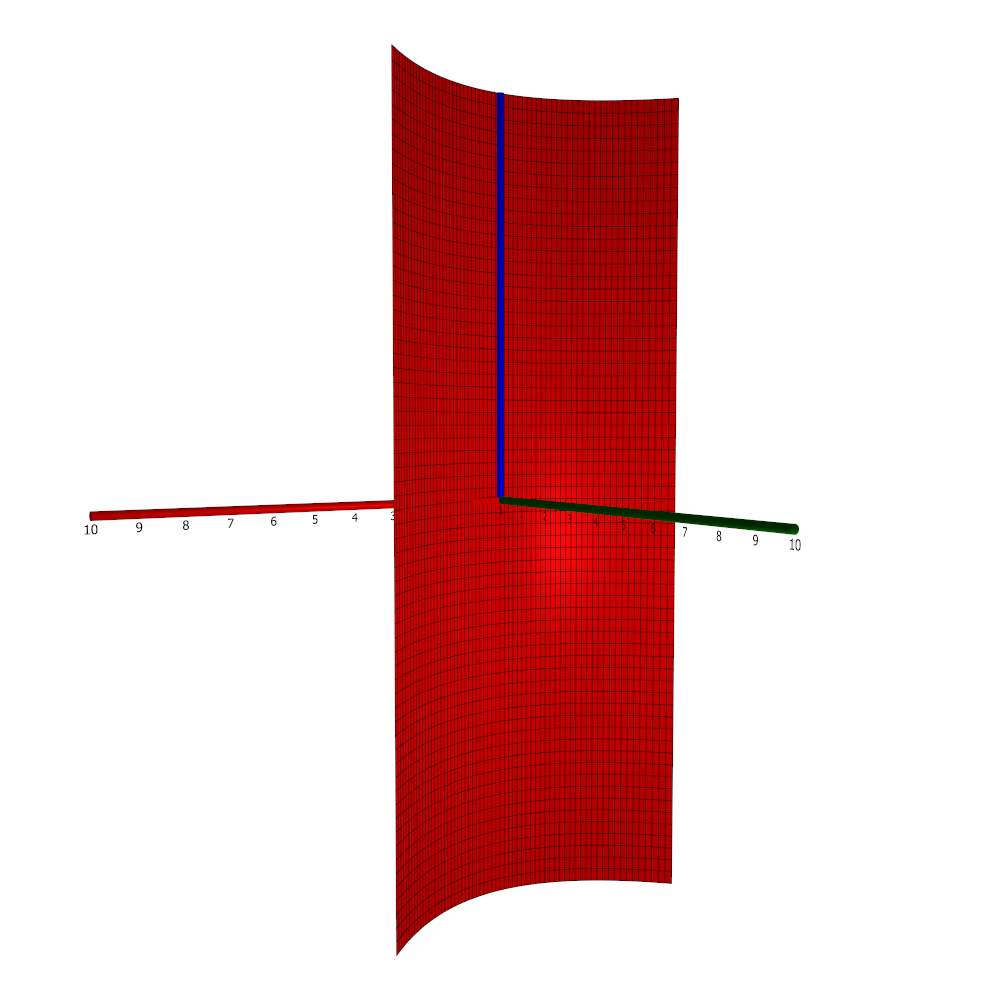
Each intersection with a plane $z = c$ is a parabola, and all such intersections are identical except for a translation in the $z$ direction. This defines the parabolic cylinder.
Parameterisation
The parabolic cylinder is the image $\mathbf{r}(\mathbb{R}^2)$ where $$\mathbf{r}(u, v)= \underline{\mathbf{e}}\begin{pmatrix}u\\au^2\\v\end{pmatrix}.$$
Properties
The following properties are with respect to the parameterisation given above.
Paramter-curve tangent vectors
The parameter-curve tangent vectors are $$\mathbf{r}_u(u,v)=\underline{\mathbf{e}}\begin {pmatrix}1\\2au\\0\end{pmatrix}, \quad\quad \mathbf{r}_v(u,v)=\underline{\mathbf{e}}\begin {pmatrix}0\\0\\1\end{pmatrix}.$$
Standard unit normal
The standard unit normal vector field is $$\mathbf{\hat{N}}(u,v)=\frac{1}{\sqrt{4a^2 u^2+1}} \underline{\mathbf{e}}\begin{pmatrix}2au\\-1\\0\end{pmatrix}.$$
Area element
The area element for the parabolic cylinder is $$dA = \sqrt{4a^2 u^2 + 1}~dudv.$$
First fundamental form
The first fundamental form is $$\mathcal{F}(u,v) = \begin{pmatrix}1+4a^2 u^2&&0\\0&&1\end {pmatrix}.$$
Second fundamental form
The second fundamental form is $$\mathcal{M}(u,v) = \begin{pmatrix}\frac{-2a}{\sqrt{4a^2 u^2+1}}&&0\\0&&0\end{pmatrix}.$$
Christoffel symbols
The Christoffel symbols are $$\Gamma^1_{\alpha\beta} = \begin{pmatrix}\frac{4a^2 u}{1+4a^2 u^2} &&0\\0&&0\end{pmatrix}, \quad\quad \Gamma^2_{\alpha\beta} = \begin{pmatrix}0&&0\\0&&0\end{pmatrix}. $$
Curvatures
The principal curvatures are $$\kappa_1 = \frac{-2a}{\left(1+4a^2 u^2\right)^{3/2}}, \quad\quad \kappa_2 = 0$$ in the directions of $(1, 0)$ and $(0, 1)$ and so the Gaussian and mean curvatures are $$K = 0, \quad\quad H = \frac{-2a}{\left(1+4a^2 u^2\right)^{3/2}},$$ respectively.
Trivia
Let $$D := \left\{\left(x, y, z\right)\in\mathbb{R}^3: z \ge y^2 \wedge y \ge x^2 \wedge x \ge z^2 \right\}.$$ Then, by elementary calculus, the volume of $D$ is $$V(D) = \int_0^1 \left({\int_{x^2}^{\sqrt[4]{x}}\left({\int_{y^2}^{\sqrt{x}}{dz}}\right)dy}\right)dx = \frac{1}{7}.$$