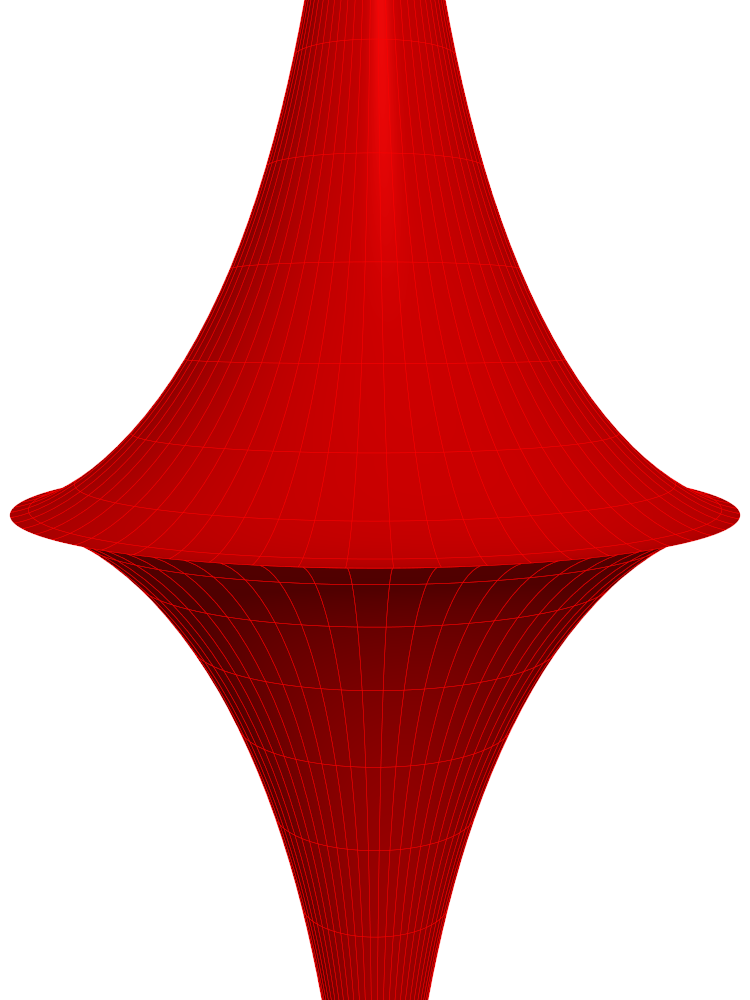
Pseudosphere
Object type: Surface
Definition
The pseudosphere of radius $r > 0$ is the image $\mathbf{r}( \R\times\left[0,2\pi\right[)$ where $$\mathbf{r}(u,v) = \basis \begin{pmatrix}r\sech u\cos v\\r\sech u\sin v\\ru-r\tanh u\end {pmatrix}.$$
The psuedosphere is not a bounded set; it does not fit inside any ball of radius $M$. Below is a part of a pseudosphere:

Parameterisation
Properties
The surface area of the pseudosphere is $$A = 4\pi r^2,$$ as is readily computed using the area element given below (compute first the area of the upper part at $z > 0$). Hence, the pseudosphere of radius $r$ has the same surface area as the usual sphere of the same radius.
The following properties are with respect to the parameterisation given above.
Parameter-curve tangent vectors
The parameter-curve tangent vectors are $$\mathbf{r}_u(u,v) = \basis \begin{pmatrix}-r\tanh u\sech u\cos v\\-r\tanh u\sech u\sin v\\r-r\sech^2 u\end{pmatrix}, \quad\quad \mathbf{r}_v(u,v) = \basis\begin{pmatrix}-r\sech u\sin v\\r \sech u\cos v\\0\end{pmatrix}.$$
Standard unit normal
The standard unit normal vector field is $$\mathbf{\hat{N}}(u,v) = |\coth u|\basis \begin{pmatrix}(\sech^2 u - 1)\cos v\\(\sech^2 u - 1)\sin v\\-\sech u\tanh u \end{pmatrix}.$$
Area element
The area element is $$dA = r^2 \sech u |\tanh u|~dudv.$$
First fundamental form
The first fundamental form of the pseudosphere is $$\mathcal{F}(u,v) = r^2 \begin{pmatrix}\tanh^2 u&&0\\0&&\sech^2 u\end{pmatrix}.$$
Second fundamental form
The second fundamental form is $$\mathcal{M}(u,v) = r |\sinh u|\sech^2 u \begin{pmatrix} -1&&0\\0&&1\end{pmatrix}.$$
Christoffel symbols
The Christoffel symbols are $$\Gamma^1_{\alpha\beta} = \sech u~\csch u\begin{pmatrix}1&&0\\ 0&&1\end{pmatrix}, \quad\quad \Gamma^2_{\alpha\beta} = -\tanh u \begin{pmatrix}0&&1\\1&&0 \end{pmatrix}.$$
Curvatures
The principal curvatures are $$\kappa_1 = -\frac{1}{r} |\csch u|, \quad\quad \kappa_2 = \frac{1}{r} |\sinh u|$$ with corresponding principal directions $(1,0)$ and $(0,1)$. Therefore, the Gaussian and mean curvatures are $$K = -\frac{1}{r^2}, \quad\quad H = \frac{1}{r}\left( |\sinh u| - |\csch u|\right).$$ Thus, the pseudosphere is a surface of constant negative curvature, which explains its name.