Torus
Object type: Surface
Definition
A torus of major radius $R > 0$ and minor radius $r > 0$ is a surface obtained as a circle of radius $r$ is rotated about a coplanar axis a distance $R$ away from its centre. (Normally, $R > r$, which will be assumed in what follows.) Below a torus of radii 4 and 1 is shown.
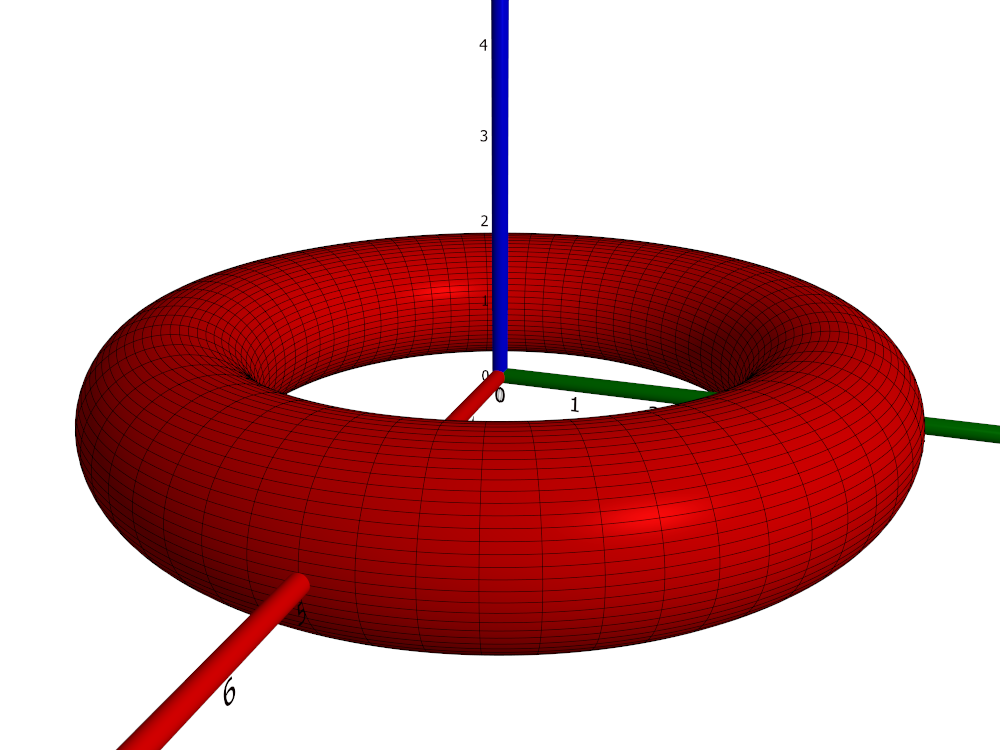
Using the Pappus–Guldinus theorems it is readily found that the area and internal volume of the torus are $A = 4\pi^2 R r$ and $V = 2\pi^2 R r^2$, respectively. (Of course, these formulae may also be readily derived naïvely from the parameterisation given below.)
Parameterisation
If the circle is centred at $(0, R, 0)$ and is rotated about the $z$ axis, the resulting torus is the image $\mathbf{r}(\left[0,2\pi\right[^2)$ where $$\mathbf{r}(u,v) = \basis\begin {pmatrix}(R+r\cos v)\cos u\\(R+r\cos v)\sin u\\r\sin v\end{pmatrix}.$$
Properties
The following properties are with respect to the parameterisation given above.
Parameter-curve tangent vectors
The parameter-curve tangent vectors are $$\mathbf{r}_u(u,v) = \basis\begin{pmatrix}-(R+r \cos v)\sin u\\(R+r\cos v)\cos u\\0\end{pmatrix}, \quad\quad \mathbf{r}_v(u,v)=\basis\begin {pmatrix}-r\sin v\cos u\\-r\sin v\sin u\\r\cos v\end{pmatrix}.$$
Standard unit normal
The standard unit normal vector field is $$\mathbf{\hat{N}}(u,v) = \basis\begin{pmatrix}\cos u \cos v\\\sin u\cos v\\\sin v\end{pmatrix}.$$
Area element
The surface area element is $$dA = r(R+r\cos v)~dudv.$$
First fundamental form
The first fundamental form is $$\mathcal{F}(u,v) = \begin{pmatrix}(R+r\cos v)^2&&0\\0&&r^2 \end{pmatrix}.$$
Second fundamental form
The second fundamental form is $$\mathcal{M}(u,v) = \begin{pmatrix}-(R+r\cos v)\cos v&&0\\0 &&-r\end{pmatrix}.$$
Christoffel symbols
The Christoffel symbols are $$\Gamma^1_{\alpha\beta} = \frac{-r\sin v}{R+r\cos v}\begin{pmatrix} 0&&1\\1&&0\end{pmatrix},\quad\quad \Gamma^2_{\alpha\beta} = \frac{(R+r\cos v)\sin v}{r}\begin{pmatrix} 1&&0\\0&&0\end{pmatrix}.$$
Curvatures
The principal curvatures are $$\kappa_1 = \frac{-\cos v}{R+r\cos v}, \quad\quad \kappa_2 = \frac{-1}{r}$$ with corresponding principal directions $(1,0)$ and $(0,1)$. Hence, the Gaussian and mean curvatures are $$K = \frac{\cos v}{r(R+r\cos v)}, \quad\quad H = \frac{-R-2r\cos v} {r(R+r\cos v)}.$$ Notice that the Gaussian curvature is positive on the 'outside' ($\cos v > 0$) and negative on the 'inside' ($\cos v < 0$). At the 'top' and 'bottom' circles, the Gaussian curvature is zero.
