Möbius strip
Object type: Surface
Definition
The Möbius strip is the surface obtained as two sides of a rectangular sheet (such as a piece of paper) are joined together in the 'opposite direction'. [If they had been joined in the 'same direction', an elliptic cylinder would be the result.] Below a Möbius strip made from a piece of paper is shown, together with a computer-made 3D surface of the same shape.
The most intriguing property of the Möbius strip is that it is a surface with only one side.
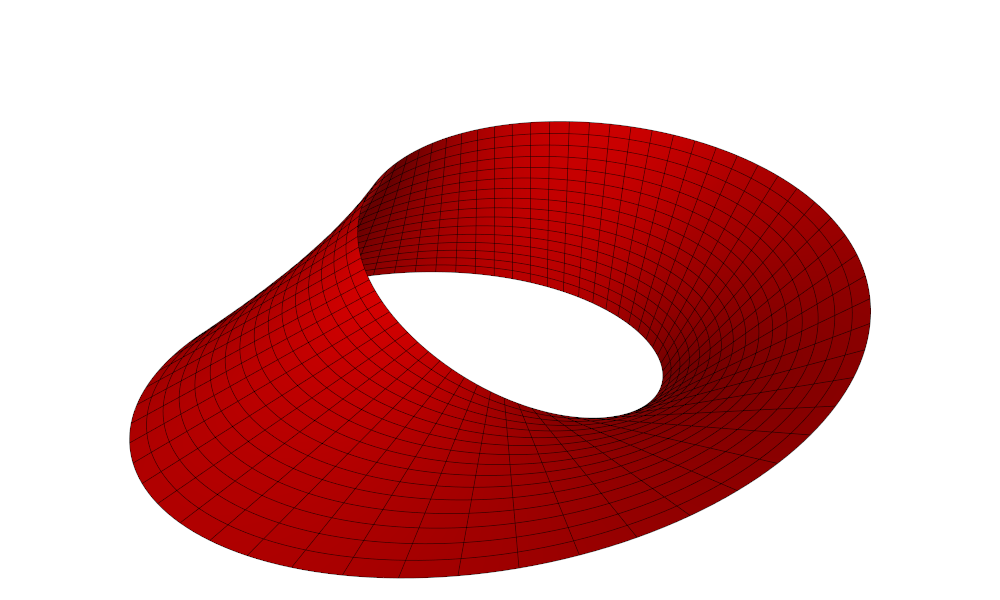
From below:

From the side:
Parameterisation
The Möbius strip shown above is the image $\mathbf{r}(\left[0,2\pi\right[\times\left[-1,1 \right])$ where $$\mathbf{r}(u,v) = \basis\begin{pmatrix}\left(1+\frac{1}{2}v\cos{\frac{u}{2}} \right)\cos u\\\left(1+\frac{1}{2}v\cos{\frac{u}{2}}\right)\sin u\\\frac{1}{2}v\sin{\frac{u}{2} }\end{pmatrix}.$$
Properties
Standard unit normal
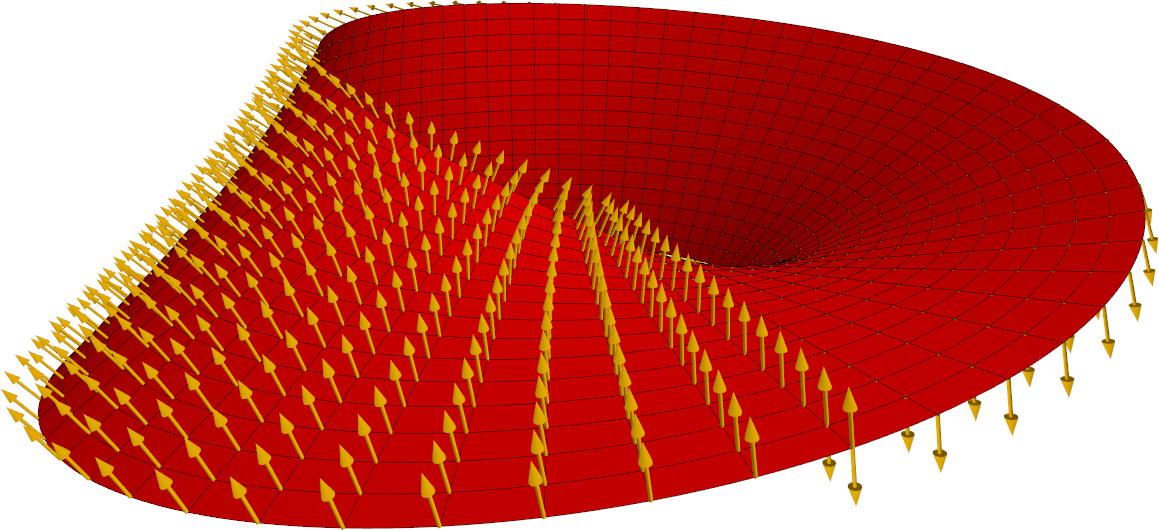
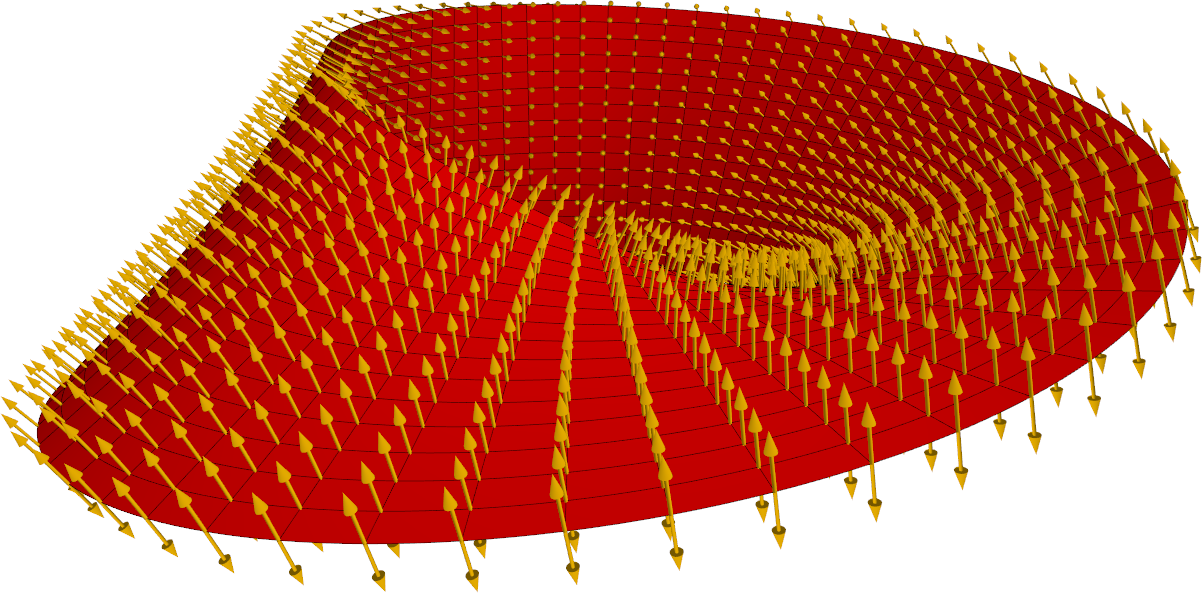
Since the Möbius strip is nonorientable, it is not possible to construct a smooth, non-vanishing normal vector field on the entire surface. Nevertheless, one can imagine that one 'cuts open' the strip somewhere along it, so that a (deformed) rectangular piece of paper is obtained. Of course, this paper has two sides, is orientable, and has such a normal vector field. The image below shows such a field, where the Möbius strip is 'cut open' at its front (bottom centre).
Obviously, one cannot talk about the 'standard unit normal vector field' of Möbius strip. Nevertheless, at each point, there is a well-defined normal direction, and so one may talk about the 'standard normal direction field' of the surface: