Elliptic paraboloid
Object type: Surface
Definition
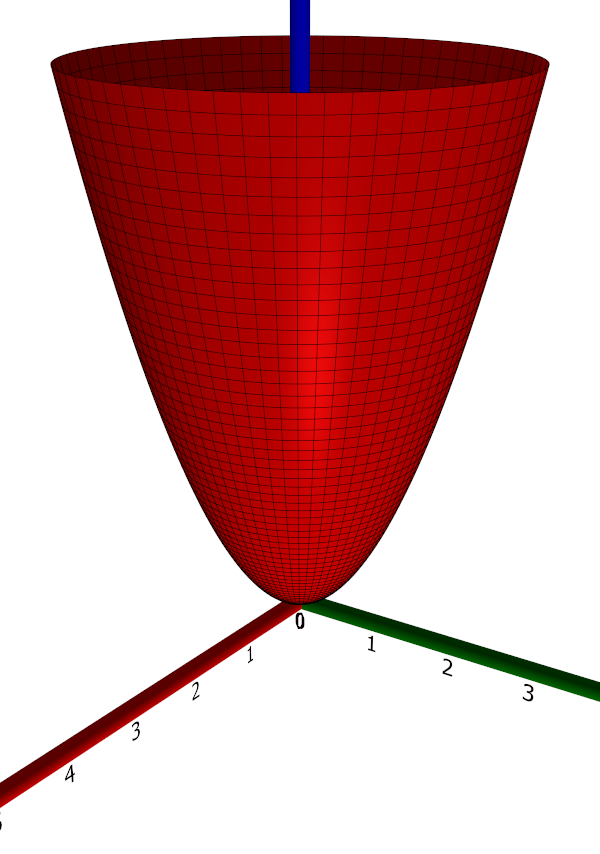
In $\mathbb{R}^3$, an elliptic paraboloid is a set of points $(x, y, z)$ satisfying the equation $$z = \left(\frac{x}{a}\right)^2 + \left(\frac{y}{b}\right)^2$$ for some constants $a, b > 0$. If $a = b$, the surface is a circular paraboloid, or a paraboloid of revolution. Every intersection with a plane $z = c_0 > 0$ is an ellipse (a circle, if $a=b$). Intersections with the planes $x=0$ and $y=0$ yield parabolae, and in the case of a circular paraboloid, the surface may be obtained by rotating a parabola about its axis of symmetry. Below, a part of the 'standard paraboloid' $z = x^2 + y^2$ is shown.
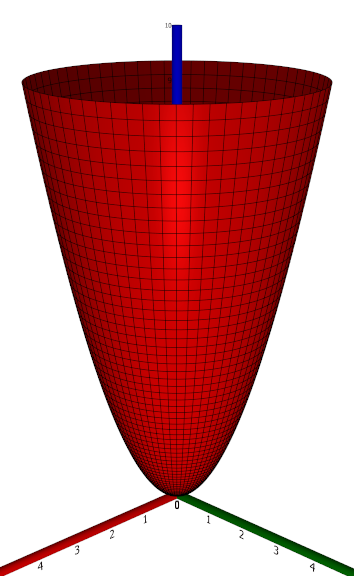
In the case of a paraboloid of revolution, every intersection with a plane containing the $z$ axis is a parabola with the $z$ axis as its axis of symmetry. Thus, they all have the same point as their foci. Hence it makes sense to talk about the 'focus' of a paraboloid of revolution.
Parameterisation
The elliptic paraboloid is the image $\mathbf{r}(D)$ where $$\mathbf{r}(u, v) = \underline{ \mathbf{e}}\begin{pmatrix}au\cos{v}\\bu\sin{v}\\u^2\end{pmatrix}$$ and $D:=\overline{\mathbb{R}^+} \times\left[0, 2\pi\right[.$ The elliptic paraboloid may also be parameterised using cartesian coordinates, which often yields simpler formulae. Indeed, since the elliptic paraboloid is the graph of the function $(x,y) \mapsto (x/a)^2 + (y/b)^2$, it is the image $\mathbf{q}(\mathbb{R}^2)$ where $$\mathbf{q}(x,y) = \underline{\mathbf{e}}\begin{pmatrix}x\\y\\\left(\frac{x}{a}\right)^2 + \left(\frac{y}{b}\right)^2\end{pmatrix}.$$
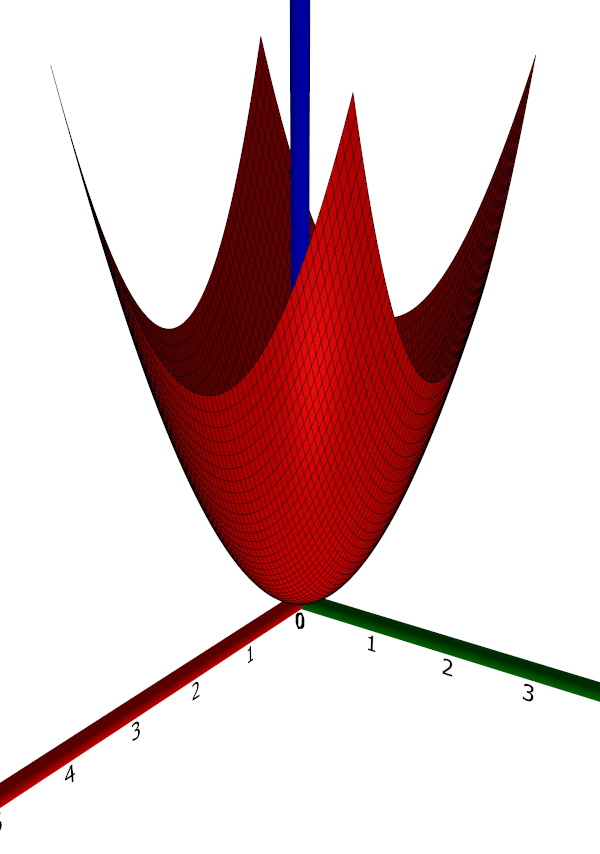
Below, the parameter curves of the two parameterisations are shown. Notice that the $\mathbf{r}$ parameterisation respects the symmetry of the parabola better than the 'cartesian' parameterisation.
Properties
All properties given below are with respect to the parameterisation $\mathbf{r}$ given above.
Parameter-curve tangent vectors
The parameter-curve tangent vectors are $$\mathbf{r}_u(u,v) = \underline{\mathbf{e}}\begin{pmatrix} a\cos{v}\\b\sin{v}\\2u\end{pmatrix}, \quad\quad \mathbf{r}_v(u,v) = \underline{\mathbf{e}}\begin {pmatrix}-au\sin{v}\\bu\cos{v}\\0\end{pmatrix}.$$
Standard unit normal
The standard unit normal vector field is $$\mathbf{\hat{N}}(u,v) = \frac{1}{\sqrt{4b^2 u^2 \cos^2 v + 4a^2 u^2 \sin^2 v + a^2 b^2}} \underline{\mathbf{e}}\begin{pmatrix}-2bu \cos{v}\\-2au \sin{v} \\ab\end{pmatrix}$$ which reduces to $$\mathbf{\hat{N}}(u,v) = \frac{1}{\sqrt{4 u^2 + a^2}} \underline {\mathbf{e}}\begin{pmatrix}-2u \cos{v}\\-2u \sin{v}\\a\end{pmatrix}$$ if $a = b$.
Area element
The area element is $$dA = u \sqrt{4b^2 u^2 \cos^2 v + 4a^2 u^2 \sin^2 v + a^2 b^2}~dudv.$$ If $a = b$, this reduces to $$dA = au \sqrt{4 u^2 + a^2}~dudv.$$
First fundamental form
The first fundamental form of the elliptic paraboloid is $$\mathcal{F}(u,v) = \begin{pmatrix}a^2\cos^2 v + b^2 \sin^2 v+4u^2 &&(-a^2 +b^2 ) u \sin v \cos v\\(-a^2 +b^2 ) u \sin v \cos v&&a^2 u^2 \sin^2 v + b^2 u^2 \cos^2 v\end{pmatrix},$$ which, if $a = b$, reduces to $$\mathcal{F}(u,v) = \begin{pmatrix}a^2 + 4u^2&&0\\0&& a^2 u^2 \end{pmatrix}.$$
Second fundamental form
The second fundamental form is $$\mathcal{M}(u,v) = \frac{1}{\sqrt{4b^2 u^2 \cos^2 v + 4a^2 u^2 \sin^2 v + a^2 b^2}} \begin{pmatrix}2ab&&0\\0&&2abu^2\end{pmatrix},$$ which, if $a = b$, reduces to $$\mathcal{M}(u,v) = \frac{1}{\sqrt{4 u^2 + a^2}} \begin{pmatrix}2a&&0\\0&&2a u^2\end{pmatrix}.$$
Christoffel symbols
Here we will only consider the case $a = b$. The Christoffel symbols are $$\Gamma^1_{\alpha\beta} = \begin {pmatrix}\frac{4u}{a^2+4u^2}&&0\\0&&\frac{-a^2u}{a^2+4u^2}\end{pmatrix}, \quad\quad \Gamma^2_{\alpha\beta}= \begin{pmatrix}0&&\frac{1}{u}\\\frac{1}{u}&&0\end{pmatrix}.$$
Curvatures
Here we will only consider the case $a = b$. Then, the principal curvatures are $$\kappa_1 = \frac{2a} {\left(a^2 + 4u^2\right)^{3/2}}, \quad\quad \kappa_2 = \frac{2}{a\sqrt{a^2 +4u^2}}$$ in the directions $(1, 0)$ and $(0, 1)$, respectively. Therefore, the Gaussian and mean curvatures are $$K = \frac{4}{\left( a^2 + 4u^2\right)^2}, \quad\quad H = \frac{4a^2+8u^2}{a\left(a^2+4u^2\right)^{3/2}}.$$
Paraboloids as Mirrors
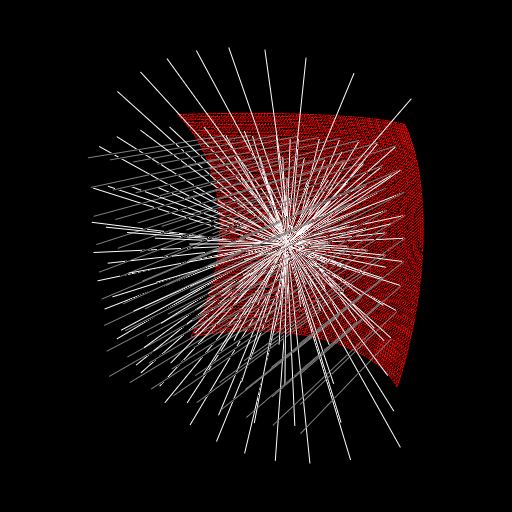
A light-ray travelling towards a mirror shaped like a paraboloid of revolution, parallel to its axis of symmetry, will be reflected in the direction towards the focus of the paraboloid, independent of where the ray hits the mirror. This makes paraboloid mirrors very useful in technical applications. Below we compare a paraboloid-shaped mirror with a spherical mirror. The spherical mirror fails to concentrate the light-rays to a single point.