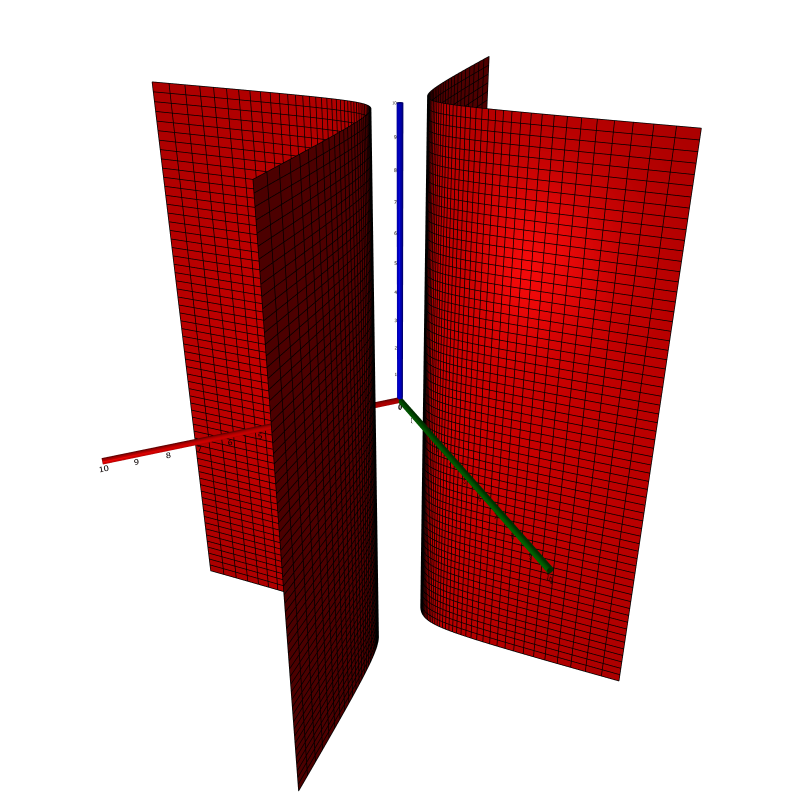
Hyperbolic cylinder
Object type: Surface
Definition
In $\mathbb{R}^3$, a hyperbolic cylinder is a set of points $(x, y, z)$ satisfying the equation $$\left(\frac{x}{a}\right)^2 - \left(\frac{y}{b}\right)^2 = 1$$ for some constants $a, b > 0$. Below, a part of a hyperbolic cylinder with $a = b = 1$ is shown.
Each intersection with a plane $z = c$ is a hyperbola, and all such intersections are identical except for a translation in the $z$ direction. This defines the hyperbolic cylinder.
Parameterisation
The part $\text{sgn}(x) = \pm 1$ of the hyperbolic cylinder is the image $\mathbf{r}( \mathbb{R}^2)$ where $$\mathbf{r}(u,v) = \underline{\mathbf{e}}\begin{pmatrix}\pm a\cosh{u} \\b\sinh{u}\\v\end{pmatrix}.$$
Properties
The following properties are with respect to the parameterisation given above for the $x > 0$ part.
Paramter-curve tangent vectors
The parameter-curve tangent vectors are $$\mathbf{r}_u(u,v) = \underline{\mathbf{e}} \begin{pmatrix}a\sinh{u}\\b\cosh{u}\\0\end{pmatrix}, \quad\quad \mathbf{r}_v(u,v) = \underline{\mathbf{e}}\begin{pmatrix}0\\0\\1\end{pmatrix}.$$
Standard unit normal
The standard unit normal vector field for the hyperbolic cylinder is $$\mathbf{\hat{N}} (u,v)=\frac{1}{\sqrt{a^2\sinh^2{u}+b^2\cosh^2{u}}}\underline{\mathbf{e}}\begin{pmatrix}b \cosh{u}\\-a\sinh{u}\\0\end{pmatrix}.$$ If $a = b$, then this reduces to $$\mathbf{\hat{N}} (u,v)=\frac{1}{\sqrt{\cosh(2u)}}\underline{\mathbf{e}}\begin{pmatrix}\cosh{u}\\-\sinh{u}\\0 \end{pmatrix}.$$
Area element
The area element is $$dA = \sqrt{a^2\sinh^2{u}+b^2\cosh^2{u}}~dudv.$$ If $a = b$, this reduces to $$dA = \sqrt{\cosh(2u)}~dudv.$$
First fundamental form
The first fundamental form of the hyperbolic cylinder is $$\mathcal{F}(u,v) = \begin {pmatrix}a^2\sinh^2{u}+b^2\cosh^2{u}&&0\\0&&1\end{pmatrix},$$ which, in the case of $a=b$, reduces to $$\mathcal{F}(u,v) = \begin{pmatrix}a^2\cosh(2u)&&0\\0&&1\end{pmatrix}.$$
Second fundamental form
The second fundamental form of the hyperbolic cylinder is $$\mathcal{M}(u,v) = \begin{pmatrix}\frac{ab}{\sqrt{a^2\sinh^2{u}+b^2\cosh^2{u}}}&&0\\0&&0\end{pmatrix},$$ which, in the case of $a = b$ reduces to $$\mathcal{M}(u,v) = \begin{pmatrix}\frac{b}{\sqrt {\cosh(2u)}}&&0\\0&&0\end{pmatrix},$$
Christoffel symbols
The Christoffel symbols are $$\Gamma^1_{\alpha\beta} = \begin{pmatrix}\frac{(a^2+b^2) \sinh(2u)}{2a^2\sinh^2{u}+2b^2\cosh^2{u}}&&0\\0&&0\end{pmatrix}, \quad\quad \Gamma^2_{\alpha \beta} = \begin{pmatrix}0&&0\\0&&0\end{pmatrix}.$$ If $a=b$, these reduce to $$\Gamma^1_{ \alpha\beta} = \begin{pmatrix}\tanh{2u}&&0\\0&&0\end{pmatrix}, \quad\quad \Gamma^2_{\alpha \beta} = \begin{pmatrix}0&&0\\0&&0\end{pmatrix}.$$
Curvatures
The principal curvature are $$\kappa_1 = \frac{ab}{\left(a^2\sinh^2{u}+b^2\cosh^2{u}\right)^ {3/2}},\quad\quad \kappa_2 = 0$$ in directions $(1,0)$ and $(0,1)$, respectively. Therefore, the Gaussian and mean curvatures are $$K = 0, \quad\quad H = \frac{ab}{\left(a^2\sinh^2{u}+b^2 \cosh^2{u}\right)^{3/2}}.$$ If $a=b$, the above formulae reduce to $$\kappa_1 = \frac{1} {a\left(\cosh(2u)\right)^{3/2}}, \quad\quad \kappa_2 = 0$$ and $$K = 0, \quad\quad H = \frac{1} {a\left(\cosh(2u)\right)^{3/2}}.$$