Hyperbolic paraboloid
Object type: Surface
Definition
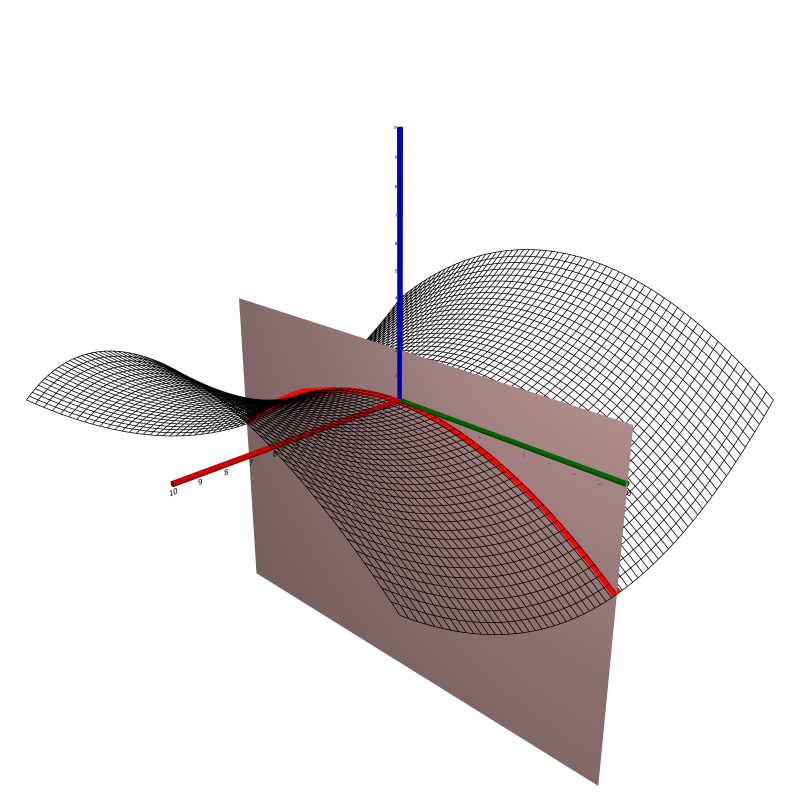
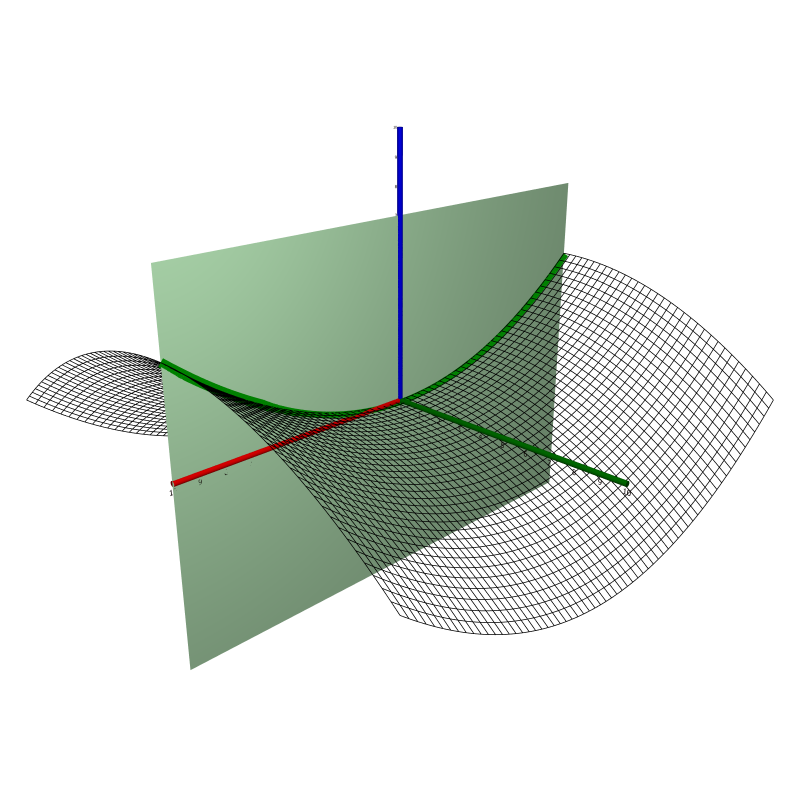
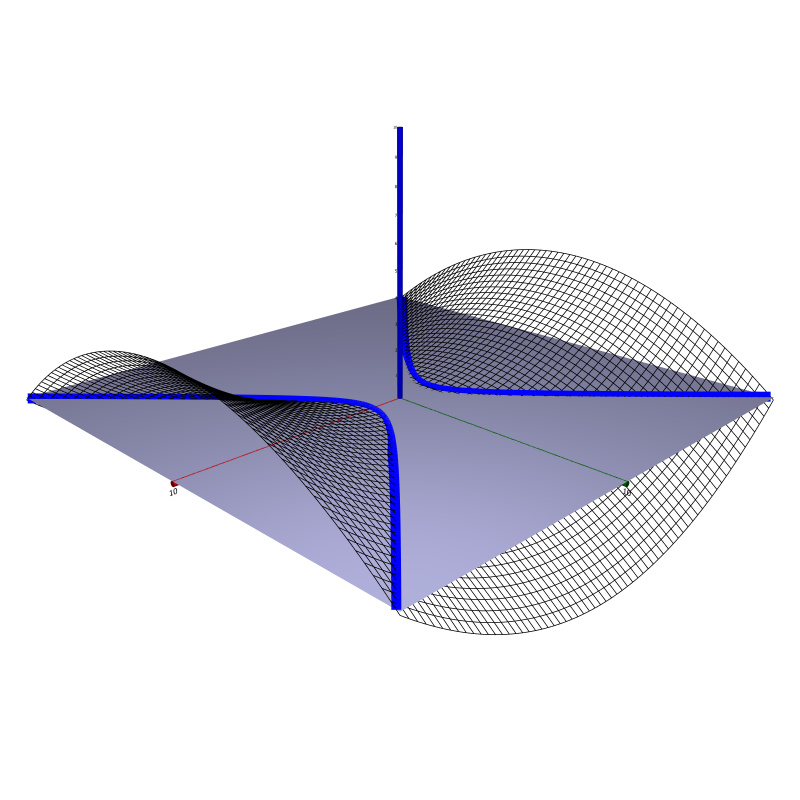
In $\R^3$, a hyperbolic paraboloid is a set of points $(x,y,z)$ satisfying the equation $$z = \left(\frac{x}{a}\right)^2 - \left(\frac{y}{b}\right)^2$$ for some constants $a, b > 0$. Every intersection with a plane $z = c_0 \ne 0$ is a hyperbola, and intersections with the planes $x = 0$ and $y = 0$ yield parabolae. Below, the hyperbolic paraboloid with $a = b = 5$ is shown.
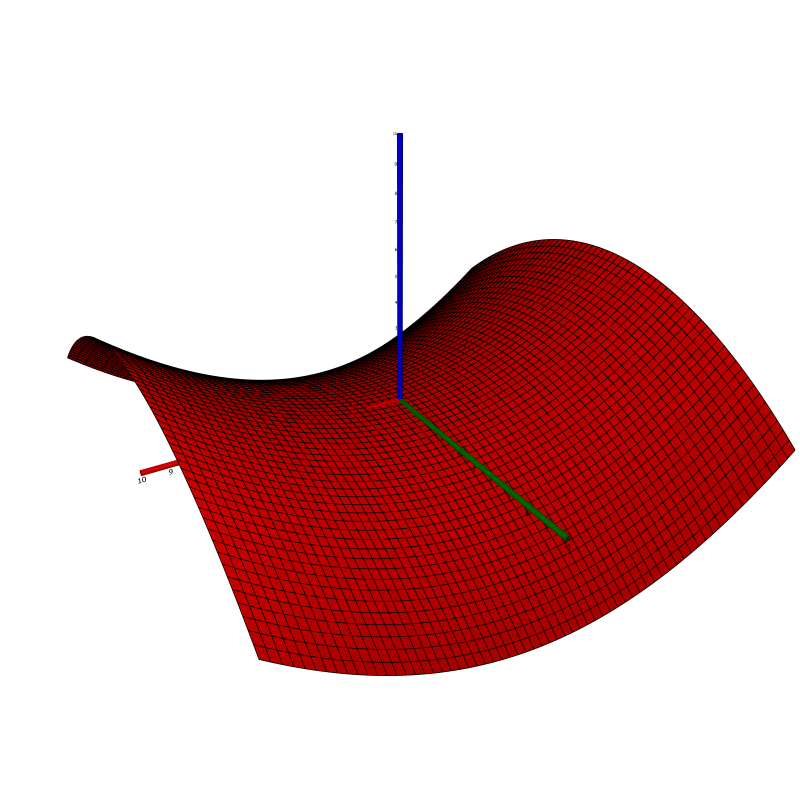
Be sure to identify the important curves obtained as intersections, as pointed out above.
Parameterisation
The hyperbolic paraboloid is the image $\mathbf{r}(\R^2)$ where $$\mathbf{r}(x,y) = \basis\begin{pmatrix}x\\y\\\left(\frac{x}{a}\right)^2- \left(\frac{y}{b}\right)^2\end{pmatrix}.$$
Properties
All properties given below are with respect to the parameterisation $\mathbf{r}$ given above.
Parameter-curve tangent vectors
The parameter-curve tangent vectors are $$\mathbf{r}_x(x,y) = \basis\begin {pmatrix}1\\0\\2x/a^2\end{pmatrix}, \quad\quad \mathbf{r}_y(x,y) = \basis\begin {pmatrix}0\\1\\-2y/b^2\end{pmatrix}.$$
Standard unit normal
The standard unit normal vector field is $$\mathbf{\hat{N}}(x,y) = \frac{1}{\sqrt{4x^2/a^4+ 4y^2/b^4+1}} \basis\begin{pmatrix}-2x/a^2\\2y/b^2\\1\end{pmatrix}.$$
Area element
The area element is $$dA = \sqrt{\frac{4x^2}{a^4} + \frac{4y^2}{b^4} + 1}~dxdy.$$
First fundamental form
The first fundamental form of the hyperbolic paraboloid is $$\mathcal{F}(x,y) = \begin {pmatrix}1 + \frac{4x^2}{a^4}&&-\frac{4xy}{a^2 b^2}\\-\frac{4xy}{a^2 b^2}&&1 + \frac{4y^2} {b^4}\end{pmatrix}.$$
Second fundamental form
The second fundamental form is $$\mathcal{M}(x,y) = \frac{2}{\sqrt{\frac{4x^2}{a^4} + \frac{4y^2}{b^4} + 1}}\begin{pmatrix}\frac{1}{a^2}&&0\\0&&-\frac{1}{b^2}\end{pmatrix}.$$
The 'multiplication function'
The surface $$z = c~xy,$$ where $c \ne 0$ is a constant, is a hyperbolic paraboloid. More specifically, it is a hyperbolic paraboloid, as defined above, with $a = b$ and rotated 45° about the $z$-axis. The most intuitive way to see this is to perform a change of linear basis in $\R^3$, from $\basis$ to $\f$, according to $$\f = \frac{1}{\sqrt{2}} \basis\begin{pmatrix}1&&1&&0\\-1&&1&&0\\ 0&&0&&\sqrt{2}\end{pmatrix}.$$ Let the new coordinates be $X, Y, Z$. Then $$\begin{pmatrix}x\\y \\z\end{pmatrix} = \frac{1}{\sqrt{2}} \begin{pmatrix}1&&1&&0\\-1&&1&&0\\0&&0&&\sqrt{2}\end{pmatrix} \begin{pmatrix}X\\Y\\Z\end{pmatrix}.$$ Therefore, $$z = \left(\frac{x}{a}\right)^2 - \left(\frac{y} {a}\right)^2 \Leftrightarrow Z = \frac{2}{a^2} XY.$$ That is, $Z = c~XY$ with $c = 2/a^2.$ Below we give the properties of the surface $$z=xy$$ with its obvious parameterisation $$\mathbf{r}(x,y) = \basis\begin{pmatrix}x\\y\\xy\end{pmatrix}.$$
Parameter-curve tangent vectors
The parameter-curve tangent vectors are $$\mathbf{r}_x(x,y) = \basis\begin{pmatrix}1\\0\\y\end {pmatrix}, \quad\quad\mathbf{r}_y(x,y) = \basis\begin{pmatrix}0\\1\\x\end{pmatrix}.$$
Standard unit normal
The standard unit normal vector field is $$\mathbf{\hat{N}}(x,y) = \frac{1}{\sqrt{1+x^2+y^2}}\basis \begin{pmatrix}-y\\-x\\1\end{pmatrix}.$$
Area element
The area element is $$dA = \sqrt{1+x^2+y^2}~dxdy.$$
First fundamental form
The first fundamental form is $$\mathcal{F}(x,y) = \begin{pmatrix}1+y^2&&xy\\xy&&1+x^2\end{pmatrix}.$$
Second fundamental form
The second fundamental form is $$\mathcal{M}(x,y) = \frac{1}{\sqrt{1+x^2+y^2}}\begin{pmatrix}0&&1\\ 1&&0\end{pmatrix}.$$
Curvatures
The Gaussian and mean curvatures are $$K = \frac{-1}{\left(1+x^2+y^2\right)^2}, \quad\quad H = \frac {-2xy}{\left(1+x^2+y^2\right)^{3/2}}.$$