Line
Object type: Space curve
Definition
In $\mathbb{R}^3$, a (straight) line through the point $\mathbf{x}_0 \in \mathbb{R}^3$ with direction $\mathbf{v}\in\mathbb{R}^3$ is the image of the parameterisation map $$t\mapsto\mathbf{x}_0+t\mathbf{v},\quad\quad\forall t\in \mathbb{R}.$$ Below, the line $\mathbf{r}(\mathbb{R})$ is shown, where $$\mathbf{r}(t) = \underline{\mathbf{e}}\begin{pmatrix}0\\1\\0\end{pmatrix} + t \underline{\mathbf{e}}\begin{pmatrix}1\\1\\1\end{pmatrix}.$$
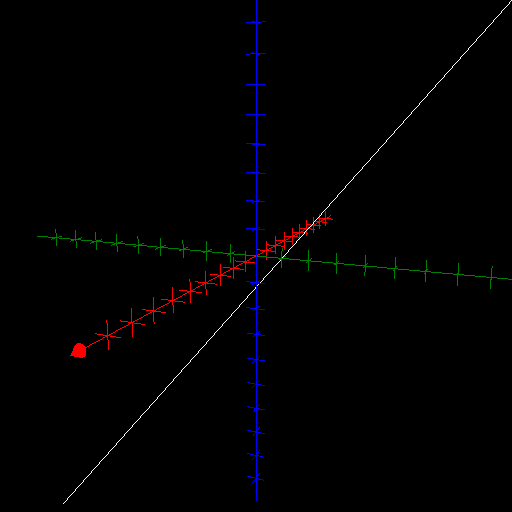
Arc Length
The arc length from the point with parameter value $t_0$ to the one corresponding to $t_0 + \Delta t$ is $\Delta t \| \mathbf{v} \|.$
Curvature
A straight line has everywhere zero curvature, $\kappa \equiv 0$.
Torsion
A straight line has everywhere zero torsion, $\tau \equiv 0$.
Examples
According to Newton's first law of motion, any object not subject to a non-vanishing net force will travel with constant velocity, thus along a straight line.
