Plane
Object type: Surface
Definition
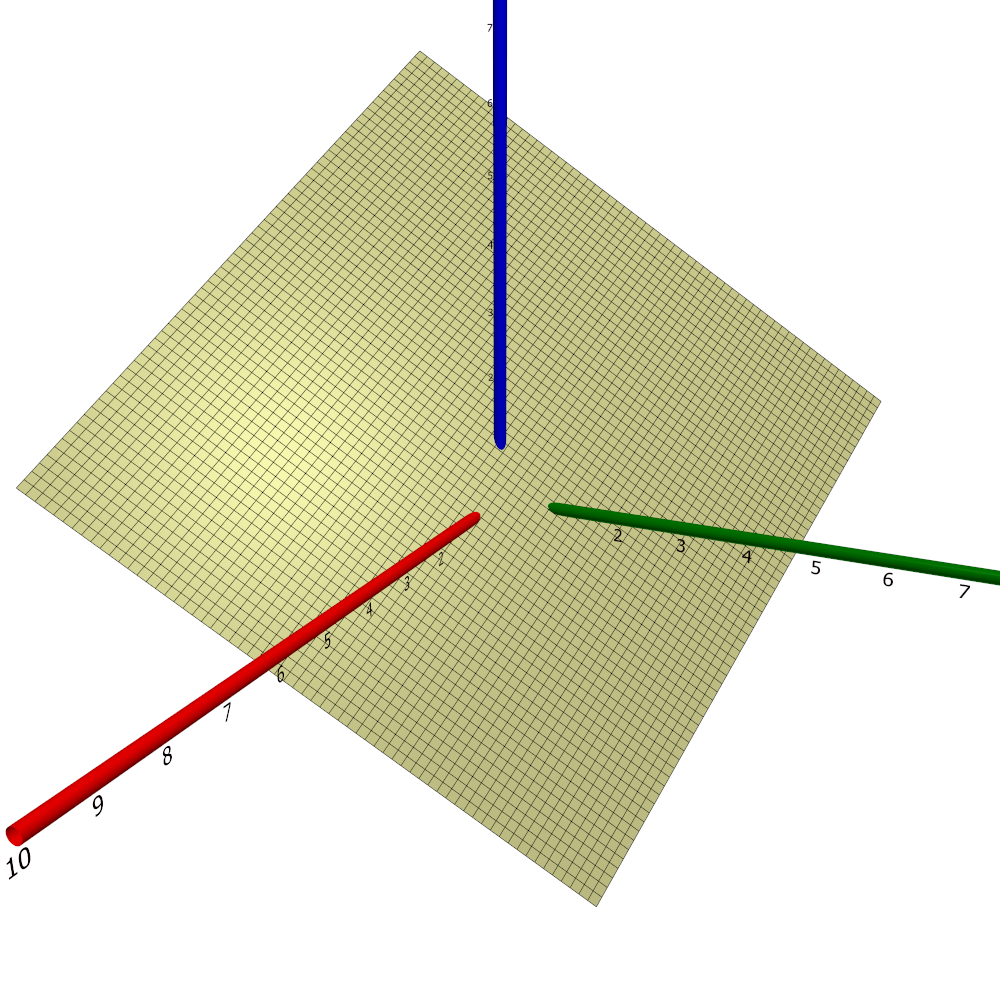
In $\R^3$, a plane is a set of points satisfying the equation $$ax+by+cz=d$$ for some $a, b, c, d \in \R$ with at least one of $a$, $b$, and $c$ non-vanishing. Below, part of the plane $x+y+z=1$ is shown.
The plane contains the origin iff $d=0$ and the normal vector of the plane is $(a,b,c)$.
Parameterisation
If $\mathbf{x}_0 \in \R^3$ is a point in the plane and if the vectors $\mathbf{u}, \mathbf{v} \in \R^3$ are parallel to the plane and linearly independent, then the plane is the image $\mathbf{r}(\R^2)$ where $$\mathbf{r}(s,t) = \mathbf{x}_0 + s\mathbf{u} + t\mathbf{v},\quad\quad \forall (s,t)\in\R^2.$$ For example, the plane given above is the image $\mathbf{r}(\R^2)$ where $$\mathbf{r}(s,t) = \basis\begin{pmatrix}0\\0\\3\end{pmatrix} + s\basis\begin{pmatrix}1\\1\\0 \end{pmatrix}+t\basis\begin{pmatrix}1\\0\\1\end{pmatrix},\quad\quad\forall(s,t)\in\R^2.$$
Properties
The following properties are with respect to the parameterisation given above.
Parameter-curve tangent vectors
The parameter-curve tangent vectors are simply $\mathbf{u}$ and $\mathbf{v}$.
Standard unit normal
The standard unit normal vector of the plane is constant, namely, $$\mathbf{\hat N} = \frac{1}{|\mathbf{u}\times\mathbf{v}|} \mathbf{u}\times\mathbf{v}.$$
Area element
The area element is $dA = |\mathbf{u}\times\mathbf{v}|~dudv$.
First fundamental form
The first fundamental form is $$\mathcal{F} = \begin{pmatrix}|\mathbf{u}|^2&&\mathbf{u} \cdot\mathbf{v}\\\mathbf{u}\cdot\mathbf{v}&&|\mathbf{v}|^2\end{pmatrix}.$$
Second fundamental form
The second fundamental form is the zero 2×2 matrix.
Christoffel symbols
All Christoffel symbols are zero.
Curvatures
Every point is an umbilic with principal curvature equal to zero. Consequently, both the Gaussian and the mean curvature are identically zero.