Ellipsoid
Object type: Surface
Definition
In $\mathbb{R}^3$, an ellipsoid is a set of points $(x,y,z)$ satisfying $$\left(\frac{x}{a}\right)^2 + \left(\frac{y}{b}\right)^2 + \left(\frac{z}{c}\right)^2 = 1$$ for some constants $a, b, c > 0$.
- If $a = b = c =: r$, we have a sphere of radius $r$.
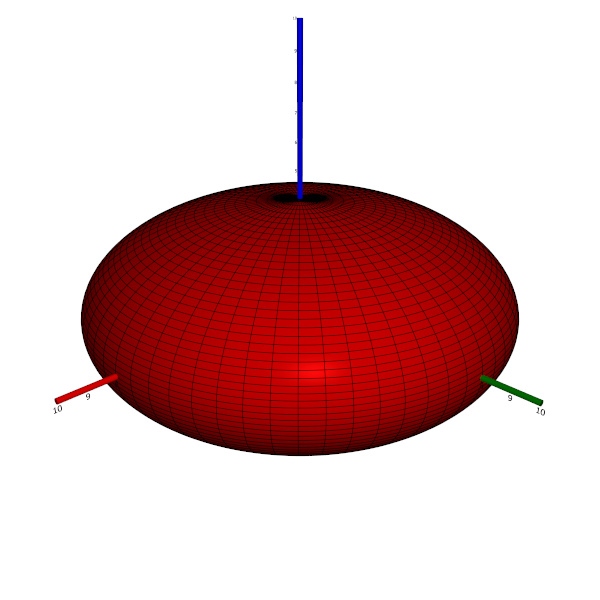
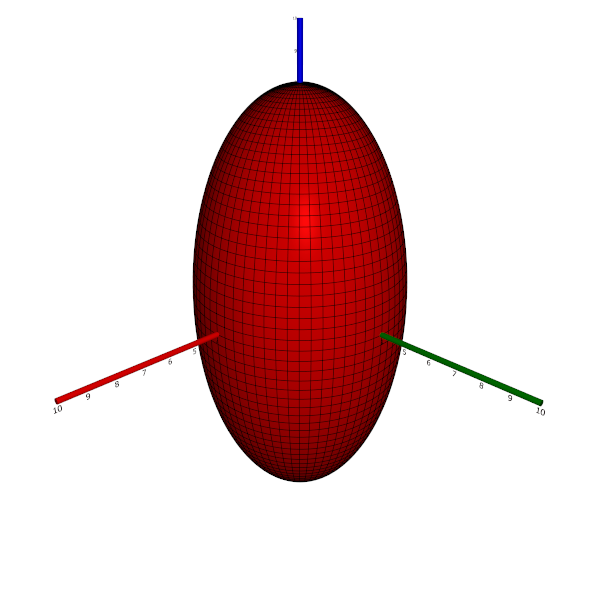
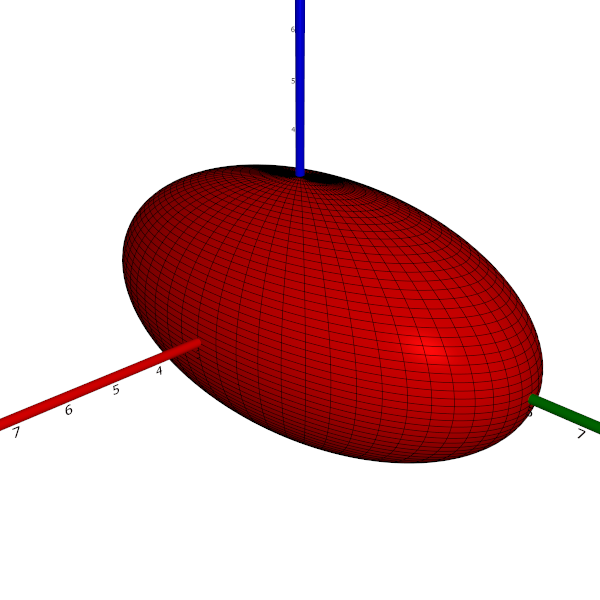
- If two of the three constants are equal, and the third one differs from the two equal constants, then the surface is a (non-spherical) ellipsoid of revolution, that is, the surface obtained as a (non-circular) ellipse is rotated about one of its axes. If the exceptional constant is smaller than the two equal constants, the ellipsoid is oblate; otherwise, it is prolate.
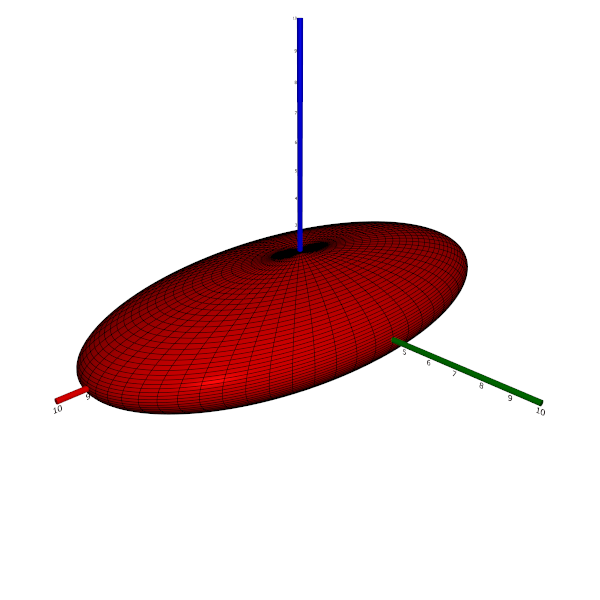
- If all three constants are distinct, we have a tri-axial ellipsoid.
Below, a prolate ellipsoid of revolution with $a = c = 3, b = 6$ is shown.
Parameterisation
The ellipsoid is the image $\mathbf{r}(D)$ where $$\mathbf{r}(\theta,\varphi) = \underline{ \mathbf{e}}\begin{pmatrix}a\sin\theta\cos\varphi\\b\sin\theta\sin\varphi\\c\cos\theta\end {pmatrix}$$ and $D := \left[0,\pi\right]\times\left[0,2\pi\right[$.
Properties
The ellipsoid is a subset of $\left[-a, a\right]\times\left[-b, b\right]\times\left[-c, c\right]$. The properties below are with respect to the parameterisation given above.
Parameter-curve tangent vectors
The parameter-curve tangent vectors are $$\mathbf{r}_\theta(\theta,\varphi) = \underline{ \mathbf{e}}\begin{pmatrix}a\cos\theta\cos\varphi\\b\cos\theta\sin\varphi\\-c\sin\theta\end {pmatrix}, \quad\quad \mathbf{r}_\varphi(\theta,\varphi) = \underline{\mathbf{e}}\begin{pmatrix} -a\sin\theta\sin\varphi\\b\sin\theta\cos\varphi\\0\end{pmatrix}.$$
Standard unit normal
The standard unit normal vector field is $$\mathbf{\hat{N}}(\theta,\varphi) = \frac{1}{\sqrt{ b^2 c^2 \sin^2 \theta\cos^2 \varphi+a^2 c^2 \sin^2\theta\sin^2 \varphi+a^2 b^2 \cos^2 \theta}} \underline{\mathbf{e}}\begin{pmatrix}bc\sin\theta\cos\varphi\\ac\sin\theta\sin\varphi\\ab\cos\theta \end{pmatrix}.$$
Area element
The area element is $$dA = \sin\theta~\sqrt{b^2c^2\sin^2\theta\cos^2\varphi+a^2c^2\sin^2\theta \sin^2\varphi+a^2b^2\cos^2\theta}~d\theta d\varphi.$$
First fundamental form
The first fundamental form of the ellipsoid is $$\mathcal{F}(\theta,\varphi) = \begin{pmatrix} a^2\cos^2\theta\cos^2\varphi+b^2\cos^2\theta\sin^2\varphi+c^2\sin^2\theta&&-a^2\sin\theta\cos\theta \sin\varphi\cos\varphi+b^2\sin\theta\cos\theta\sin\varphi\cos\varphi\\-a^2\sin\theta\cos\theta\sin \varphi\cos\varphi+b^2\sin\theta\cos\theta\sin\varphi\cos\varphi&&a^2\sin^2\theta\sin^2\varphi+b^2\sin^2 \theta\cos^2\varphi\end{pmatrix}.$$
Second fundamental form
The second fundamental form is $$\mathcal{M}(\theta,\varphi) = \frac{-abc}{\sqrt{b^2c^2\sin^2\theta \cos^2\varphi+a^2c^2\sin^2\theta\sin^2\varphi+a^2b^2\cos^2\theta}}\begin{pmatrix}1&&0\\0&&\sin^2\theta \end{pmatrix}.$$